
(This article was originally published on 6/25/2018 as “VARs Explained in 300 Words, Without Equations or Vector Analysis.” Some edits have been made.)
In my experience working at Power Plants, operators generally fall into two categories when it comes to understanding reactive power (VARs): Those who sort of have a fuzzy understanding but cannot explain it and those who really have no idea.
While that may be a bit of an exaggeration as there are undoubtedly many operators who do understand VARs, I believe that one of the barriers for those who do not understand this topic is math. Every discussion of reactive power invariably brings up a myriad of equations, trigonometry, phase angles and other imposing mathematical elements. This can leave one’s head spinning and still with the question: What is reactive power really?
I am going to break it down without a mathematical analysis. As you will see, the key is the magnetic fields in an alternating current (AC) system.
Alternating current power systems rely on magnetic fields to work. A transformer, motor or generator cannot work without magnetic fields. The very principle of operation of these devices is totally dependent on those magnetic fields.
Where do these magnetic fields come from? Current flow.
Power, both real power and reactive power, is comprised of volts and amps. Since the voltage is the same for both, we can focus on the current flow. A portion of the total current flow is for the megawatts, which represents the consumption of power. The additional current is the current required to create the magnetic fields. This current is out of phase with the megawatt current and flows into and out of the system. As with the megawatts current, this megavar current is delivered by the generators.
Here is an analogy that I call the Wheelbarrow Analogy:
Consider the scenario in Figure 1. There is a wheelbarrow loaded with, let’s say, pumpkins. We wish to move this load of MW from Point A to Point B. As you know, to move a loaded wheelbarrow, you must set up the conditions to move it, i.e., lift the wheelbarrow handles.

As shown in Figure 2, this will allow you to move the load of MW to Point B. Once you reach your destination you then lower the wheelbarrow handles, as shown in Figure 3.
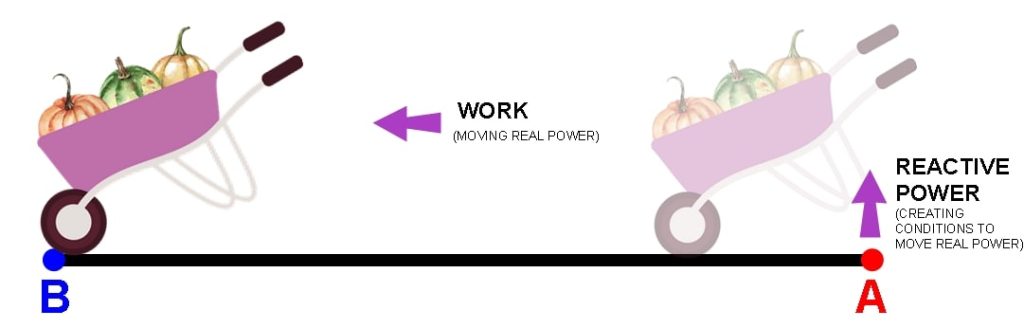
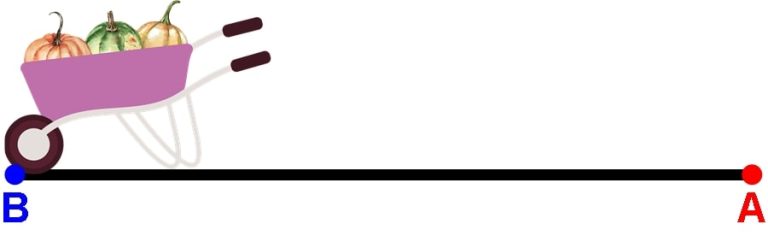
The end result: You have done real work by moving the load. What, though, was the net result of lifting the wheelbarrow handles at Point A and lowering them at Point B? Zero! Yet this action was crucial to delivering the load.
Relating to AC power systems, the portion of the current that is delivered by the generators to create the magnetic fields “disappears” if the system is turned off, i.e., it did no work. But it was a required condition to allow the electrical MW to flow through the system and do real work.
In summary, real power (megawatts) is from active current and relates to energy consumption (heat from a heating element, light from a bulb, torque on a motor, etc.); reactive power (megavars) is from passive current and corresponds to storage and retrieval of energy rather than consumption (this storage and retrieval results in the expanding and collapsing magnetic fields). There is obviously much more to the topic, such as power factor, leading versus lagging, etc. But for those wishing to get their head around understanding what VARs do, the Wheelbarrow Analogy should do the trick.
One final note: Many people will use the beer mug analogy, where the beer is the MW and the foam on top is the MVAR. I feel this falls short of truly representing reactive power because the foam is not required to create the drinkable beer, but reactive power is required to transfer real power on an AC system.